Question

The graph of f(x) = x2 is translated to form g(x) = (x – 5)2 + 1. Which graph represents g(x)?

Answer 1

The graph would be translated 5 units right and 1 unit up, giving an upward facing parabola with a vertex at (5, 1).

Step-by-step explanation:
Since 5 was subtracted from x before it was squared, this means a horizontal translation 5 units. Since it was subtracted, this means it was translated right 5 units.

The 1 added at the end means it was translated 1 unit up as well.

This is in vertex form, y=a(x-h)^2 + k, where (h, k) is the vertex; h corresponds with 5 and k corresponds with 1, so the vertex is at (5, 1).

Answer 2

Function f(x) is translated 5 units to the right and 1 unit upwards to get g(x) shown below.

Step-by-step explanation:

We are given that,

The function
`f(x)=x^2` is translated to form the function
`g(x)=(x-5)^2+1`.

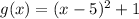So, we see that,

The function f(x) is translated 5 units to the right which gives the function
`(x-5)^2`.

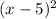Further, this function is translated to 1 unit upwards which gives the function g(x).

That is, the function f(x) is translated 5 units to the right and 1 unit upwards to get g(x).

Thus, the graph of g(x) is shown below.