Question

Tyler read 2/15 of a book on Monday, 1/3 of it on Tuesday, 2/9 of it on Wednesday and 3/4 of the remainder on Thursday. If he still has 14 pages left to read on Friday, how many pages are there in the book?

Answer 1

Answer: Total number of pages are 60 there in the book.

Step-by-step explanation: Let us assume total number of pages by x.

On Monday 2/15 of total pages were read that is = 2/15x pages

On Tuesday = 1/3 x.

On Wednesday = 2/9 x

Remaining pages on Thursday = x-2/15x-1/3 x -2/9 x

On Thursday total pages were read= 3/4 of the remainder = 3/4 ( x-2/15x-1/3 x -2/9 x).

Remaining pages on Friday = 3/4 ( x-2/15x-1/3 x -2/9 x).

We are given that one Friday 14 pages left.

Therefore,

3/4 ( x-2/15x-1/3 x -2/9 x) =14

`(3)/(4)\left(x-(2)/(15)x-(1)/(3)x-(2)/(9)x\right)=14`

Multiplying both sides by 4, we get

`4* (3)/(4)\left(x-(2)/(15)x-(1)/(3)x-(2)/(9)x\right)=14* 4`

`3\left(x-(2)/(15)x-(1)/(3)x-(2)/(9)x\right)=56`

`(14)/(15)x=56`

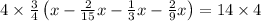
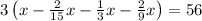
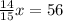
Multiplying both sides by 15, we get

`15 *(14)/(15)x=56* 15`

`14x=840`

`(14x)/(14)=(840)/(14)`

`x=60`

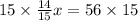
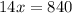
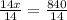
Total number of pages are 60 there in the book.

Answer 2

Fractions are normally parts of a whole thing such that they complement it. In this case, monday= 2/15 of the book was read, Tuesday= 1/3 , wednesday =2/9, Thus for the three days he will have read a fraction of (2/15+1/3+2/9) =31/45. The remainder will be 1- 31/45= 14/45, so on Thursday he read 3/4 × 14/45 = 7/30. On friday he read a fraction of 14/45 - 7/30 = 7/90.
Therefore, a fraction of 7/90 is equivalent to 14 pages. Thus the whole book was 14 × 90/7 =180 pages
= 180 pages