Question

What is the solution to 4log4(x+8)=4^2

Answer 1

ANSWER


`x = 248`

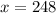
Step-by-step explanation

The given logarithmic equation is,


`4 log_(4)(x + 8) = {4}^(2)`


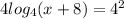
We divide through by 4 to get,



`log_(4)(x + 8) = 4`

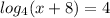
Let us take the antilogarithm of both sides to base 4 to obtain,


`x + 8 = {4}^(4)`

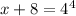
We evaluate the expression on the right hand side to obtain,


`x + 8 = 256`

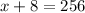
We group like terms to obtain,


`x = 256 - 8`

This simplifies to,


`x = 248`
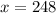
The value of x is 248.

Answer 2

assuming that's log base 4

4log4(x+8) = 4^2
log4(x+8) = 4^2/4
log4(x+8) = 4
x+8 = 4^4
x+8 = 256
x = 256 - 8
x = 248