Question

Why does multiple of 3 add up digits trick work?

Answer 1

You must be referring to the quick way to determine whether a given integer is divisible by 3; that is, 3 divides an integer
`x` whenever the digits of
`x` sum to a multiple of 3.

Suppose
`x` has
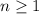
`n\ge1` digits. We can expand it as a sum of the numbers in any given digits place by the corresponding power of 10. For example, if
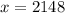
`x=2148`, we can write


`2148=2*10^3+1*10^2+4*10^1+8*10^0`

More generally, if


`x=d_(n-1)d_(n-2)\ldots d_1d_0`

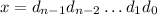
(where
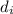
`d_i` denotes the numeral in the
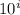
`10^i`-th's place), then we have the expansion


`x=d_(n-1)10^(n-1)+d_(n-2)10^(n-2)+\cdots+d_110^1+d_0`

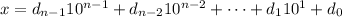
Notice that for any integer
`k`, we have


`10^k-1=\underbrace{99\ldots99}_{k\text{ 9s}}`

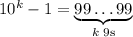
which is clearly divisible by 3. So from each power of 10 in the expansion of
`x`, we can add and subtract 1, then rearrange the terms of the sum:


`x=d_(n-1)10^(n-1)+\cdots+d_110^1+d_0`

`x=d_(n-1)(10^(n-1)-1+1)+\cdots+d_1(10^1-1+1)+d_0`

`x=d_(n-1)(10^(n-1)-1)+\cdots+d_1(10^1-1)+(d_(n-1)+\cdots+d_1+d_0)`

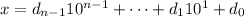
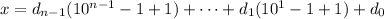
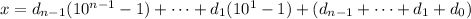
We know
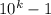
`10^k-1` is divisible by 3, which means the remainder upon dividing
`x` by 3 is just the sum of the digits of
`x`. If this remainder is divisible by 3, then so must be the original number,
`x`.

Back to our previous example: if
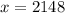
`x=2148`, then we have the expansion


`2148=2*10^3+10^2+4*10+8`

`2148=2(999+1)+(99+1)+4(9+1)+8`

`2148=2*999+99+4*9+(2+1+4+8)`

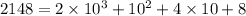
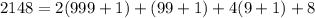
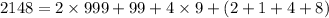
Dividing through by 3, we get a remainder of
`2+1+4+8=15`, which is divisible by 3, and so 2148 must also be a multiple of 3.

In case for some reason you're not convinced 15 is a multiple of 3, you can apply the same trick:


`15=10+5`

`15=9+1+5`

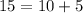
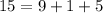
Dividing through by 3 leaves a remainder of
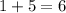
`1+5=6`, which is also a multiple of 3, so that 15 must be, too.