Answer: It will take 5 billion years for the parent isotope to get reduced to one-sixteenth of its original amount.
Step-by-step explanation:
Initial amount of an isotope =
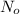
Amount left after the radio decay = N=
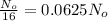
Decay constant=
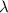
Half life of the sample:
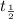 =1.25 billion years
=1.25 billion years
Years pass before a sample of potassium-40 contains one-sixteenth the original amount of parent isotope be ,t= T
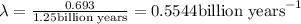
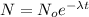
![\ln[(N_o)/(16)]=\ln[N_o]-0.5544 \text{billion years}^(-1)* T](https://img.qammunity.org/2019/formulas/chemistry/high-school/ljm7fdwcui2ird56yq9ypggrjh3k8vsrq6.png)
![\ln[(1)/(16)]=-0.5544 \text{billion years}^(-1)* T](https://img.qammunity.org/2019/formulas/chemistry/high-school/r5p9omlxslah8bumrcvnp8lvp7ghn88e28.png)
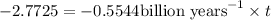
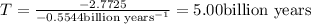
It will take 5 billion years for the parent isotope to get reduced to one-sixteenth of its original amount.