Question

If your speed triples, you need __________ times the distance to stop

Answer 1

Speed is a scalar quantity given by the rate of change in distance. Thus, it is given by distance covered divided by the time taken to cover the distance.
Speed= distance/time
therefore, speed is directly proportional to the distance covered if time taken is kept constant, such that an increase in distance causes a corresponding increase in speed and vice versa, hence if the speed triples then you will need thrice times the distance to stop.

Answer 2

9 Times

Step-by-step explanation:

The stopping distance of a car (or any traveling object) is proportional to the square of the speed of the car.

This is a consequence of the work-kinetic energy theorem, which states that the work done on the car is equal to its loss of kinetic energy:

`W=K_i-K_f`

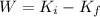
Since the final speed of the car is zero, its final kinetic energy, so we can write:

`W=K_i\\Fd=(1)/(2)mv^2`

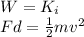
where

F is the force that stops the car (the force of friction)

d is the stopping distance

m is the mass of the car

v is the initial speed of the car

As we see from the equation, the stopping distance (d) depends on the square of the speed (
`v^2`). Therefore, it the speed is tripled, the stopping distance will acquire a factor
`3^2 = 9`, so we will need 9 times the distance to stop.