Question

Ella has 0.5 lbs of sugar. How much water should she add to make the following concentrations? Tell Ella how much syrup she will have in each case. 20%, 25% and 1.5% syrup?

Answer 1

1. 20% - add 2 lbs of water to get 2.5 lbs of syrup

2. 25% - add 1.5 lbs of water to get 2 lbs of syrup

3. 1.5% - add 32.833 lbs of water to get 33.333 lbs of syrup

Explanation:

Ella has 0.5 lbs of sugar. Let x lbs be the amount of water Ella should add to get the syrup.

1. 20% syrup:

0.5 lbs - 20%

x+0.5 lbs - 100%

Write a proportion:

`(0.5)/(x+0.5)=(20)/(100)\\ \\0.5\cdot 100=(x+0.5)\cdot 20\\ \\50=20x+10\\ \\20x=50-10\\ \\20x=40\\ \\x=2\ lbs`

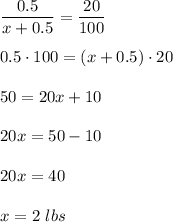
To get 20% syrup Ella should add 2 lbs of water. The total weight of strup is 2.5 lbs.

2. 25% syrup:

0.5 lbs - 25%

x+0.5 lbs - 100%

Write a proportion:

`(0.5)/(x+0.5)=(25)/(100)\\ \\0.5\cdot 100=(x+0.5)\cdot 25\\ \\50=25x+12.5\\ \\25x=50-12.5\\ \\25x=37.5\\ \\x=1.5\ lbs`

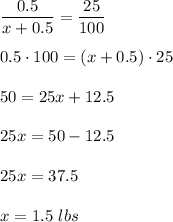
To get 25% syrup Ella should add 1.5 lbs of water. The total weight of strup is 2 lbs.

3. 1.5% syrup:

0.5 lbs - 1.5%

x+0.5 lbs - 100%

Write a proportion:

`(0.5)/(x+0.5)=(1.5)/(100)\\ \\0.5\cdot 100=(x+0.5)\cdot 1.5\\ \\50=1.5x+0.75\\ \\1.5x=50-0.75\\ \\1.5x=49.25\\ \\x=(49.25)/(1.5)\approx 32.833\ lbs`

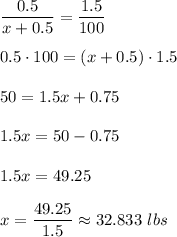
To get 1.5% syrup Ella should add 32.833 lbs of water. The total weight of strup is 33.333 lbs.