Question

Which of the following represents the general equation for the geometric sequence? -1, -2, -4, ... an = 1 · 2n - 1 an = -2n - 1 an = 2n - 1 an = 1 · 2n + 1

Answer 1

-1,-2,-4

an = a1 * r^(n - 1)
a1 = first term = -1
r = common ratio = 2

so the equation would be : an = -1 * 2^(n - 1)

Answer 2

`a_(n) =  - 2^(n-1)`.

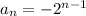Explanation:

Given : geometric sequence -1, -2, -4, ...

To find : Which of the following represents the general equation for the geometric sequence.

Solution : We have given

Geometric sequence -1, -2, -4, ...

By the formula for general equation :
`a_(n) = a_(1) *r^(n-1)`.

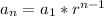Where,
`a_(n)` = last term.

`a_(1)` = first term.

r = common ratio.

r ( common ratio ) =
`(second\term)/(first\term)`.

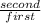In -1, -2, -4, ...

`a_(1)` = -1.

r ( common ratio ) =
`(-2)/(-1)`.

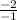r ( common ratio ) =2.

Plug the values in formula

`a_(n) =  (-1) * 2^(n-1)`.

`a_(n) =  - 2^(n-1)`.

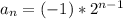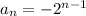Therefore,
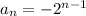`a_(n) =  - 2^(n-1)`.