Question

Noelle stands at the edge of a cliff and drops a rock. The height of the rock, in meters, is given by the function f(x)=−4.9x^2+17 , where x is the number of seconds after Noelle releases her rock. Cesar, who is standing nearby on the ground, throws a rock straight up in the air. The height of Cesar’s rock, in meters, is given by the function g(x)=−4.9x^2+13x , where x is the number of seconds after he releases his rock. There is a moment when the rocks are at the same height.

What is this height?

can anyone help me asap please I would appreciate it very much?

PLEASE HELP ME

Answer 1

I think that the height is 4 feet tall 

Answer 2

Answer: This height is 8.719 meters.

Explanation:

Since we have given that

The height of rocks after Noelle releases her rock is given by

`f(x)=-4.9x^2+17`

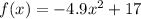
Here, x is the number of seconds.

The height of rocks after Cesar releases her rock is given by

`g(x)=-4.9x^2+13x`

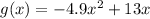
According to question, there is a moment when the rocks are at the same height.

So, our equation becomes

`f(x)=g(x)\\\\-4.9x^2+17=-4.9x^2+13x\\\\17=13x\\\\x=(17)/(13)\\\\x=1.3\ seconds`

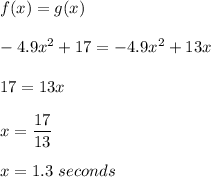
Height after 1.3 seconds would be same.

So, this height would be

`f(x)=-4.9x^2+17\\\\f(1.3)=-4.9(1.3)^2+17=8.719`

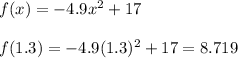
Hence, this height is 8.719 meters.