For your first question, remember that in euclidean geometry the sum of the interior angles of a triangle is always 180°. So if we have a triangle with angles

,

, and

,
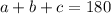
.
The angles of our triangle measure 90°, 60°, and 60°; so lets add them:
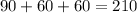
Since the sum of the angles of our triangle
is not 180°, we can conclude that
none triangle with those angle's measures can be constructed.
For our second one, we are going to use the triangle inequality theorem; it says that for any triangle the sum of the lengths of any tow sides must be greater or equal than the length of the other side.
So, the lengths of our sides are 14 cm, 8 cm, and 5 cm. Lest add tow of them and compare if the result is greater or equal than the other side:
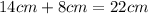
since 22 cm is greater or equal than 5 cm, so far so good.
Next pair:
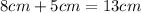
, and notice that 13 cm is not greater or equal than 14 cm. So our triangle violates the triangle inequality theorem; therefore,
none triangle can be constructed with those side's measurements.
For our last questions we are going the use the triangle inequality theorem as well. So lets add tow sides and compare if the result is grater or equal than the other side:
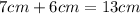
and
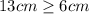
so far so good.
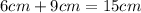
and

so far so good.
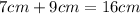
and
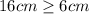
so far so good.
Since the measures of the sides of our triangles satisfy the triangle inequality theorem, we can conclude that
more than one triangle can be constructed with those side's measures.