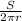Answer:
Option d is correct.
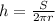
Explanation:
Lateral Surface Area of a Cylinder is directly proportional to the radius and the height of the cylinder.
The formula for the Lateral Surface Area of Cylinder is given by;
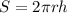
where
S represents the lateral surface Area
r is the radius of the cylinder and
h is the height of the cylinder.
To solve for h:
we have;
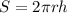
Divide both sides by
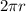 we have;
we have;
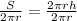
Simplify:
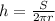
therefore, the height of the cylinder (h) =