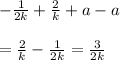Question

In quadratic drag problem, the deceleration is proportional to the square of velocity

Answer 1

Part A

Given that
`a= (dv)/(dt) =-kv^2`

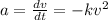
Then,


`\int dv= -kv^2\int dt \\ \\ \Rightarrow v(t)=-kv^2t+c`

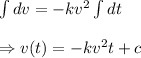
For
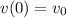
`v(0)=v_0`, then


`v(0)=-kv^2(0)+c=v_0 \\ \\ \Rightarrow c=v_0`

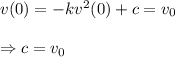
Thus,
`v(t)=-kv(t)^2t+v_0`

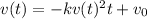
For
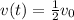
`v(t)= (1)/(2) v_0`, we have


`(1)/(2) v_0=-k\left( (1)/(2) v_0\right)^2t+v_0 \\ \\ \Rightarrow (1)/(4) kv_0^2t=v_0- (1)/(2) v_0= (1)/(2) v_0 \\ \\ \Rightarrow kv_0t=2 \\ \\ \Rightarrow t= (2)/(kv_0)`


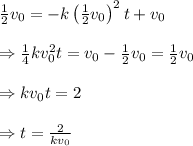
Part B

Recall that from part A,


`v(t)= (dx)/(dt) =-kv^2t+v_0 \\ \\ \Rightarrow dx=-kv^2tdt+v_0dt \\ \\ \Rightarrow\int dx=-kv^2\int tdt+v_0\int dt+a \\ \\ \Rightarrow x=- (1)/(2) kv^2t^2+v_0t+a`

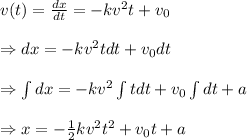
Now, at initial position, t = 0 and
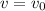
`v=v_0`, thus we have


`x=a`

and when the velocity drops to half its value,
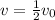
`v= (1)/(2) v_0` and
`t= (2)/(kv_0)`

Thus,


`x=- (1)/(2) k\left( (1)/(2) v_0\right)^2\left( (2)/(kv_0) \right)^2+v_0\left( (2)/(kv_0) \right)+a \\ \\ =- (1)/(2k) + (2)/(k) +a`

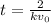
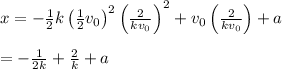
Thus, the distance the particle moved from its initial position to when its velocity drops to half its initial value is given by


`- (1)/(2k) + (2)/(k) +a-a \\ \\ = (2)/(k) - (1)/(2k) = (3)/(2k)`