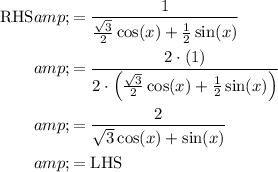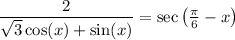
Right-hand side
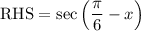
Since
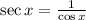 , it follows that
, it follows that
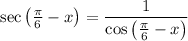
So we can rewrite
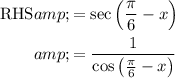
We have a cosine difference identity for the denominator:
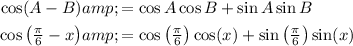
Since
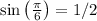 and
and
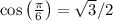 , we have
, we have
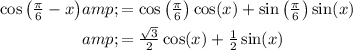
Using this in the right-hand side
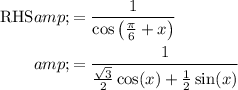
Notice how we have tiny denominators of 2.If we multiply the numerator and denominator of the entire fraction, we will deal with those twos, as 2 will distribute and cancel.