Answer : The correct option is, 5
Solution : Given,
Mass of nickel-59 = 0.17 g
Mass of cobalt-59 = 5.27 g
Equation for the radioactive decay of nickel-59 is :
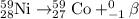
Now, we have to calculate the initial amount of nickel-59, we are using the stoichiometry of the reaction and moles of the reactant and product.
Formula used :
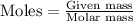
Moles of
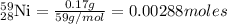
Moles of
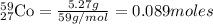
By stoichiometry of the reaction,
1 mole of
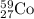 is produced by 1 mole
is produced by 1 mole
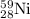
So, 0.089 moles of
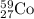 will be produced by =
will be produced by =
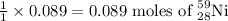
Amount of
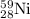 decomposed will be = 0.089 moles
decomposed will be = 0.089 moles
Initial amount of
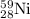 will be = Amount decomposed + Amount left = (0.00288 + 0.089)moles = 0.09188 moles
will be = Amount decomposed + Amount left = (0.00288 + 0.089)moles = 0.09188 moles
Now, to calculate the number of half lives, we use the formula :
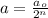
where,
a = amount of reactant left after n-half lives = 0.00288 moles
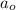 = Initial amount of the reactant = 0.09188 moles
= Initial amount of the reactant = 0.09188 moles
n = number of half lives
Now put all the given values in above equation, we get
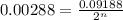
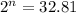
Taking log on both sides, we get
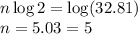
Therefore, '5' number of half-lives have passed since the meteorite formed .