Answer with Step-by-step explanation:
We are given that sound intensity I form a spherical source
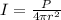
Where r=Distance from the source of sound
P=Power of the sound
When r=0 then the intensity is undefined at source.
When r=infinity
Then , the intensity,
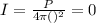
Intensity is inversely proportional to distance r from the source of sound.
It means when the distance from the source increases then the intensity decreases.
When r increases and goes to infinity then the intensity approach to zero.