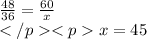Answer:
The Answer is
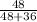
Explanation:
Let me draw this triangle for you as you haven't drawn the triangle.
To find the side SR , you have shown that
ΔPST ~(is similar to)ΔPRQ [AA]
As, you know when triangles are similar their sides are proportional.
So,

You can solve this question using other way also
As, ST║RQ
then
 ⇒ [ if in a triangle a line is parallel to a side
⇒ [ if in a triangle a line is parallel to a side
intersecting the other two sides in distinct points then the ratio of the segments where the line segment intersects the other two sides are same.]