ANSWER
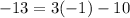
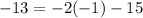
Step-by-step explanation
The given system is
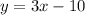
and
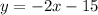
The solution to the system is
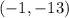
This implies that,
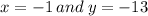
To justify this solution means we substitute,
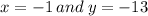
into the given system.
When substitute into the first equation we get
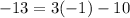
When we substitute into the second equation, we obtain,
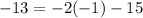
The correct answer is B.