Question

Please Please help me with this  problem

Answer 1

Assuming that both cyclists are traveling AWAY from each other with the same starting point, consider the following:

Let us denote the speed of the first bicyclist by
`s` (measured in miles per hour). Then, the speed of the second bicyclist must be
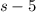
`s-5` (miles per hour).

To verify this, assign an arbitrary number, say 17 mph, to the first bicyclist. Since the first bicyclist is always 5 mph faster than the second, we must have 17 - 5 = 12 mph as the second speed.

At the 0th hour,
- first bicyclist has traveled 0 miles
- second bicyclist has traveled 0 miles
- distance between both = 0 miles

At the 1st hour,
- first bicyclist has traveled
`1* s=s` miles
- second bicyclist has traveled
`-1*(s-5)=-s+5` miles (note the negative sign here. Since they are traveling in opposite directions, they must have opposite signs of each other in distances traveled)
- distance between both =
`s-(-s+5)` =
`s+s-5` =
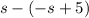
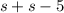
`2s-5` miles

At the second hour,
- first bicyclist has traveled
`2s` miles
- second bicyclist has traveled
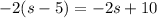
`-2(s-5)=-2s+10` miles
- distance between both =
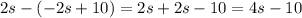
`2s-(-2s+10)=2s+2s-10=4s-10` miles

According to the question statement, both of them are 70 miles apart at the second hour, i.e.

`4s-10=70`
such that solving this gives:

`4s=70+10`

`4s=80`

`s= (80)/(4)`

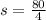
`s=20` mph

Therefore, their rates are as follows:
- first bicyclist = 20 mph
- second bicyclist = 20 - 5 = 15 mph

Answer 2

The work become much simpler if you do it in a table. Hope this helps!!