Question

A 1570 kg car skidding due north on a level frictionless icy road at 156 km/h collides with a 2245.1 kg car skidding due east at 120 km/h in such a way that the two cars stick together. At what angle (−180◦ ≤ θ ≤ +180◦ ) East of North do the two coupled cars skid off at?

Answer 1

θ = 47.75º East of North.

Step-by-step explanation:

• Assuming no external forces acting during the collision, total momentum must be conserved.
• Since momentum is a vector, if we project it along E-W and N-S axes, the momentum components along these axes must be conserved too.
• So, for the N-S axis, we can write the following equation:

`p_(Northo) = p_(Northf) (1)`

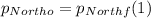
• Since the car moving due east has no speed component along the N-S axis, the initial momentum along this axis is simply:

`p_(Northo) = m_(1) * v_(1o) (2)`

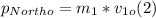
where m₁ = 1570 kg, v₁₀ = 156 km/h

• In order to work with the same units, we need to convert the speed in km/h to m/s, as follows:

`v_(1o) = 156 km/h *(1000m)/(1 km)*(1h)/(3600s) = 43.3 m/s (3)`

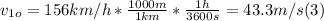
• Replacing by the values in the left side of (1), we get:

`p_(Northo) = m_(1) * v_(1o) = 1570 kg* 43.3 m/s = 67981 kg*m/s (4)`

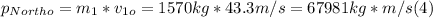
• Since the collision is inelastic, both cars stick together, so we can write the right side of (1) as follows:

`p_(Northf) = (m_(1) + m_(2))* v_(fNorth) = 3815.1 kg* v_(fNorth) (5)`

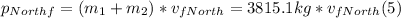
• From (4) and (5) , we can solve for VfNorth:

`V_(fNorth) = (67981kg*m/s)/(3815.1kg) = 17.8 m/s (6)`

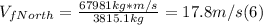
• We can repeat exactly the same process for the E-W axis:

`p_(Easto) = p_(Eastf) (7)`

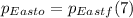
• Since the car moving due north has no speed component along the E-W axis, the initial momentum along this axis is simply:

`p_(Easto) = m_(2) * v_(2o) (8)`

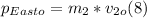
• As we did with v₁₀, we need to convert v₂₀ from km/h to m/s, as follows:

`v_(2o) = 120 km/h *(1000m)/(1 km)*(1h)/(3600s) = 33.3 m/s (9)`

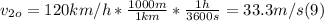
• Replacing by the values in the left side of (7), we get:

`p_(Easto) = m_(2) * v_(2o) = 2245.1 kg* 33.3 m/s = 74762 kg*m/s (10)`

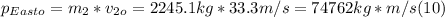
• Since the collision is inelastic, both cars stick together, so we can write the right side of (7) as follows:

`p_(Eastf) = (m_(1) + m_(2))* v_(fEast) = 3815.1 kg* v_(fEast) (11)`

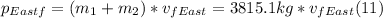
• From (10) and (11) , we can solve for VfEast:

`V_(fEast) = (74762 kg*m/s)/(3815.1kg) = 19.6 m/s (12)`

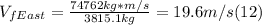
• In order to find the angle East of North of the velocity vector, as we know the values of the horizontal and vertical components, we need just to apply a little bit of trigonometry, as follows:

`tg \theta = (V_(fEast))/(V_(fNorth) ) = (19.6)/(17.8) = 1.1 (13)`

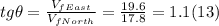
• The angle θ, East of North, is simply tg⁻¹ (1.1):

θ = tg⁻¹ (1.1) = 47.75º E of N.