Question

Eight students are competing for 1st, 2nd, 3rd, and 4th violin chair in the school’s orchestra. How many different ways can all four chairs be filled?

Answer 1

8 different ways, im pretty sure

Answer 2

There are eight students. Each student is competing for 1st, 2nd, 3rd and 4th violin chair. We will use permutation to solve this problem.

When we have 'n' items and we want to find the number of ways 'k' items can be ordered. Then we use the permutation formula which states:

`^nP_(k)=(n!)/((n-k)!)`

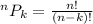
Therefore,

`=^8P_(4)=(8!)/((8-4)!)`

=
`(8!)/((4)!)`

=
`(8 * 7* 6* 5* 4!)/(4!)`

=
`{8 * 7* 6* 5}`

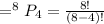
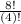
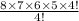
= 1680

Therefore, in 1680 different ways can all four chairs be filled.