Question

For the velocity fields given below, determine:

a) whether the flow field is one-, two-, or three-dimensional,
b) whether the flow is steady or unsteady, and why. (The quantities a and b are constants.)
1. V = [ay2e−bt]i
2. V = ax^2i + bxj + ck
3. V = axyi - bytj
4. V = axi - byj + ctk

Answer 1

Answer and Explanation: A fluid flow is steady when its properties (velocity, pressure and others) do not change over time: P = P(x,y,z), with P being any of the properties.

So, an unsteady flow does depend upon time: P = P(x,y,z,t).

1. V = [
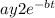`ay2e^(-bt)`]i : This velocity field is one-dimension, because there is only the component in the x-direction and unsteady, because it is dependent upon the variable time (t);

2. V =
`ax^(2)i+bxj+ck` : is a three-dimensional field, because there is one component for each direction (x, y and z) and is steady, since it's independent of time;

3. V = axyi - bytj : is a 2-dimensional field, and since it changes with time, it is unsteady;

4. V = axi - byj + ctk : is a 3-dimensional field and the flow is unsteady;