Question

Rationalize the denominator of sqrt -49 over (7 - 2i) - (4 + 9i)

Answer 1

`\sqrt{ (-49)/((7-2i)-(4+9i) ) }`

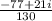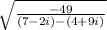
This one is quite the deal, but we can begin by distributing the negative on the denominator and getting rid of the parenthesis:


`( √(-49))/(7-2i-4-9i)`

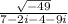
See how the denominator now is more a simplification of like terms, with this I mean that you operate the numbers with an "i" together and the ones that do not have an "i" together as well. Namely, the 7 and the -4, the -2i with the -9i.
Therefore having the result:


`( √(-49) )/(3-11i)`

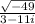
Now, the
`√(-49)` must be respresented as an imaginary number, and using the multiplication of radicals, we can simplify it to
`√(49) √(-1)`
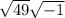
This means that we get the result 7i for the numerator.


`(7i)/(3-11i)`

In order to rationalize this fraction even further, we have to remember an identity from the previous algebra classes, namely:
`x^2 - y^2 =(x+y)(x-y)`
The difference of squares allows us to remove the imaginary part of this fraction, leaving us with a real number, hopefully, on the denominator.


`(7i (3+11i))/((3-11i)(3+11i))`

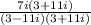
See, all I did there was multiply both numerator and denominator with (3+11i) so I could complete the difference of squares.
See how
`(3-11i)(3+11i)= 3^2 -(11i)^2` therefore, we can finally write:


`(7i(3+11i))/(3^2 - (11i)^2 )`

I'll let you take it from here, all you have to do is simplify it further.
The simplification is quite straightforward, the numerator distributed the 7i. Namely the product
`7i(3+11i) = 21i+77i^2`.
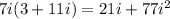
You should know from your classes that i^2 = -1, thefore the numerator simplifies to
`-77+21i`
You can do it as a curious thing, but simplifying yields the result:

`(-77+21i)/(130)`