Question

You are assigned the design of a cylindrical, pressurized water tank for a future colony on Mars, where the acceleration due to gravity is 3.71 meters per second per second. The pressure at the surface of the water will be 150 KPa , and the depth of the water will be 14.4 m . The pressure of the air in the building outside the tank will be 88.0 KPa .

Find the net downward force on the tank's flat bottom, of area 2.15 m2 , exerted by the water and air inside the tank and the air outside the tank.

Answer 1

Answer: F = 6262.2 kN

Step-by-step explanation: Pressure is defined as force per area. But pressure varies according to the depth of a fluid: in air, it decreases the higher the altitude, while in water, it increases the deeper you go.

So, at the bottom of the tank, besides the pressure of air inside the tank and air outside the tank, there is pressure of water due to its depth.

Pressure due to the depth is calculated as

`P=h.\rho.g`

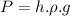
h is the depth in m

ρ is density of the fluid, in this case is water, so ρ = 997 kg/m³

g is acceleration due to gravity, which, in this case, is 3.71 m/s²

Then, pressure at the bottom of the tank due to variation in depth is

`P=14.4(997)(3.71)`

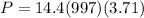
P = 53263.73 Pa or 53.26 kPa

Assuming positive referential is downward, all pressures at the bottom point down, so total or resultant pressure is:

`P_(r)=P_(1)+P_(2)+P_(3)`

`P_(r)=150+88+53.26`

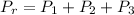
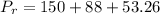
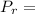`P_(r)=` 291.26 kPa

At last, pressure is force per area:

`P=(F)/(A)`

`F=P.A`

`F_(r)=P_(r).A`

`F_(r)=291.26.10^(3)(2.15)`

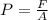
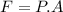
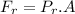
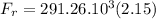
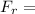`F_(r)=` 626209 N or 626.2 kN

At the cylindrical tank's flat bottom, net force has magnitude 626.2 kN.