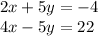
There are many ways of solving a system of equation, a very used one is by elimination of variables, which consists in eliminating one of the variables by combining the equations.
Let's do the following combination: (eq 1) + (eq 2)
This means that we add each term vertically:
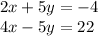
⇒
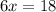
When I said "add vertically" means that you add the first term of the first equation with the first term of the second equation. The second term of the first equation with the second term of the second equations, and so on.
This allowed us to remove the "y" temporarily so we can get a linear one-variable equation we can easily solve:
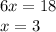
Now that we know the value of "x", we can plug it in any of the starting equations and get "y":
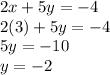
Therefore, our answer looks like this:
