Question

A tree that is 3 feet tall is growing at a rate of 1 foot per year. A 5-foot tree is growing at a rate of 0.75 foot per year.

The ordered pair (t, h) represents the time in years, t, at which the trees are at height, h.

Which ordered pair represents the number of years elapsed when the trees are at the same height?

(6, 9) (12, 14) (7, 10.25) (8, 11)

Answer 1

h1=3+t
h2=5+3t/4
3+t=5+3t/4
-2=3t/4-4t/4
-2=-t/4
8=t
[(8,11)]

Answer 2

Given the height of tree is 3 feet tall

Let
`h_(1)` be the height of 3 feet tall tree which is growing at the rate of 1 foot per year.

Let the rate at which tree is growing be 't'.

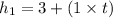`h_(1) = 3+( 1 * t)` = 3+ t

Given the height of tree is 5 foot.

Let
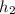`h_(2)` be the height of 5 foot tall tree which is growing at the rate of 0.75 foot per year.

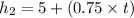`h_(2) = 5+( 0.75 * t)` = 5+0.75t

We have to find the the number of years elapsed when the trees are at the same height.

Therefore,
`h_(1)=h_(2)`

`3+t = 5+0.75t`

`3-5 = 0.75t-t`

`-2=-0.25t`

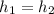
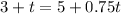
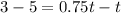
t = 8.

Therefore,

As
`h_(1)=3+t`

`h_(1)=3+8`

`h_(1)= 11`

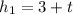
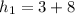
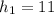
Therefore, (8,11) represents the number of years elapsed when the trees are at the same height.