Answer: The required binomial that is a factor of f(x) is (x - 5).
Step-by-step explanation: We are given the binomials (x + 1), (x + 4), (x − 5), and (x − 2).
We are to select the one that is a factor of the following polynomial function :
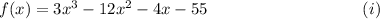
Factor theorem : If the value of a function p(x) is zero at x = a, then (x - a) is a factor of p(x).
Now, substituting x = -1 in equation (i), we get
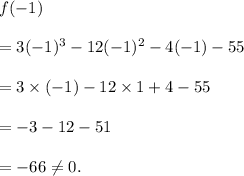
So, (x + 1) is NOT a factor f(x).
Substituting x = -4 in equation (i), we get
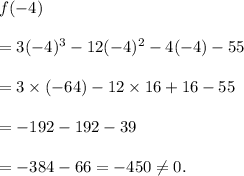
So, (x + 4) is NOT a factor f(x).
Substituting x = 5 in equation (i), we get
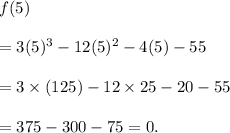
So, (x - 5) is a factor f(x).
Substituting x = 2 in equation (i), we get
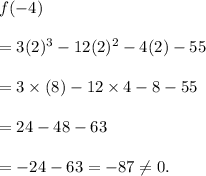
So, (x - 2) is NOT a factor f(x).
Thus, the required binomial that is a factor of f(x) is (x - 5).