Answer:
13.75%
Explanation:
Givens:
- APR first days: 0%.
- APR afterwards: 14.04%.
We have to find the effective interest rate, which is defined as:
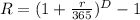
First days:
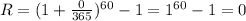
Afterwards:
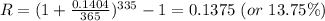
So, the effective interest would be the difference between these two, which is 13.75%.