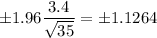Question

An experiment using 35 guinea pigs is set up to study the weight of the pigs after injecting them with a drug. If the population mean is 23.5 grams with a standard deviation of 3.4 grams, what is the margin of error of the sample mean?

Answer 1

1.1264

Explanation:

Given : An experiment using 35 guinea pigs is set up to study the weight of the pigs after injecting them with a drug.

To Find: If the population mean is 23.5 grams with a standard deviation of 3.4 grams, what is the margin of error of the sample mean?

Solution:

n = 35

`\sigma = 3.4`

Confidence interval = 95%. So, z =1.96

Margin of error =
`z * (\sigma)/(√(n))`

Margin of error =
`1.96* (3.4)/(√(35))`

Margin of error =
`1.1264`

Hence the margin of error of the sample mean is 1.1264.

Answer 2

Margin of Error =
`\pm 0.1904`

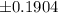
Explanation:

We are given the following information in the question:

Population mean, μ = 23.5 grams

Population standard deviation, σ = 3.4 grams

Sample size, n = 35

Alpha, α = 0.05

Formula:

`\text{Margin of Error} = z\displaystyle(\sigma)/(√(n))`

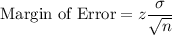
where z is the z-critical at 0.05 level of significance.

Putting the values, we get:

z-critical at 0.05 level of significance =
`\pm 1.96`

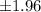
Margin of Error =

`\pm 1.96\displaystyle(3.4)/(√(35)) = \pm 1.1264`