Question

Suppose 83% of all students taking a beginning programming course fail to get their first program to run on first submission. Consider a group of 7 such students,where each student's success is independent from the other and the chance each student fails on their first try is consistent. (Round answers to three decimal places.)

(a) all fail on their first submissions
(b) at least four fail on their first submissions
(c) less than four fail on their first submissions
Continuing to use this binomial model,
(d) what is the mean number who will fail?
(e) what are the variance and standard deviation of the number who will fail?

Answer 1

a) 0.271 = 27.1% probability that all fail on their first submissions

b) 0.981 = 98.1% probability that at least four fail on their first submissions

c) 0.019 = 1.9% probability that less than four fail on their first submissions

d) The mean number who will fail is 5.81.

e) The variance is 0.988, while the standard deviation is 0.994.

Explanation:

For each student, there are only two possible outcomes. Either their first program run will fail, or it wont. The probability of the first program run of a student failing is independent of the first program run of other students. So we use the binomial probability distribution to solve this question.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

In which
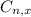`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

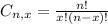
And p is the probability of X happening.

The expected value of the binomial distribution is:

`E(X) = np`

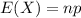
The variance of the binomial distribution is:

`V(X) = np(1-p)`

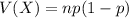
The standard deviation of the binomial distribution is:

`√(V(X)) = √(np(1-p))`

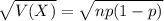
In this question, we have that:

83% of all students taking a beginning programming course fail to get their first program to run on first submission. Sample of 7 students. This means that
`p = 0.83, n = 7`

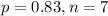
(a) all fail on their first submissions

This is
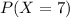`P(X = 7)`. So

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 7) = C_(7,7).(0.83)^(7).(0.17)^(0) = 0.271`

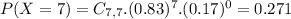
0.271 = 27.1% probability that all fail on their first submissions;

(b) at least four fail on their first submissions

This is

`P(X \geq 4) = P(X = 4) + P(X = 5) + P(X = 6) + P(X = 7)`

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 4) = C_(7,4).(0.83)^(4).(0.17)^(3) = 0.082`

`P(X = 5) = C_(7,5).(0.83)^(5).(0.17)^(2) = 0.239`

`P(X = 6) = C_(7,6).(0.83)^(6).(0.17)^(1) = 0.389`

`P(X = 7) = C_(7,7).(0.83)^(7).(0.17)^(0) = 0.271`

`P(X \geq 4) = P(X = 4) + P(X = 5) + P(X = 6) + P(X = 7) = 0.082 + 0.239 + 0.389 + 0.271 = 0.981`

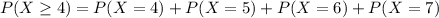
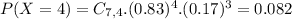
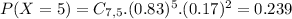
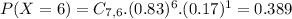
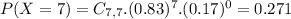
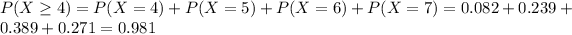
0.981 = 98.1% probability that at least four fail on their first submissions.

(c) less than four fail on their first submissions

Either less than four fail, or at least four fail. The sum of the probabilities of these events is 100% = 1. So

`P(X < 4) + P(X \geq 4) = 1`

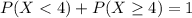
From b),
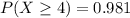`P(X \geq 4) = 0.981`. So

`P(X < 4) = 1 - P(X \geq 4) = 1 - 0.981 = 0.019`

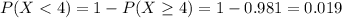
0.019 = 1.9% probability that less than four fail on their first submissions.

(d) what is the mean number who will fail?

Expected value, so

`E(X) = np = 7*0.83 = 5.81`

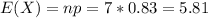
The mean number who will fail is 5.81.

(e) what are the variance and standard deviation of the number who will fail?

Variance:

`V(X) = np(1-p) = 7*0.83*0.17 = 0.988`

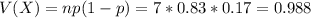
Standard deviation:

`√(V(X)) = √(0.9877) = 0.994`

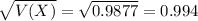
The variance is 0.988, while the standard deviation is 0.994.