Question

For the hypothetical reactions 1 and 2, k1 = 102 and k2 = 10–4. 1. a2(g) + b2(g) 2ab(g) 2. 2a2(g) + c2(g) 2a2c(g) 3. a2c(g) + b2(g) 2ab(g) + (1/2)c2(g) what is the value for k for reaction 3?

Answer 1

Answer is: valeu for K is 10⁴.
Reaction 1: A₂ + B₂ → 2AB.
Reaction 2: 2A₂ + C₂→ 2A₂C.
Reaction 3: A₂C + B₂ → 2AB + 1/2C.
Reaction 3 is reaction 1 + 1/2 reverse reaction 2.
K₁ = 10².
K₂ = 10⁻⁴.
K₃ = 10² · √10⁴ = 10² · 10² = 10⁴.

Answer 2

Answer : The value of K for the reaction 3 will be,
`10^4`

Explanation :

The chemical reactions are :

(1)
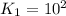
`a_2(g)+b_2(g)\rightarrow 2ab(g)`;
`K_1=10^2`

(2)
`2a_2(g)+c_2(g)\rightarrow 2a_2c(g)`;
`K_2=10^(-4)`

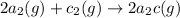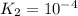
The final chemical reaction is :

(3)
`a_2c(g)+b_2(g)\rightarrow 2ab(g)+(1)/(2)c_2(g)`
`K_3=?`

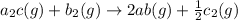
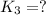
Now we have to calculate the value of
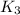`K_3` for the final reaction.

Now reverse equation 2 and multiply by (1/2) and then add both the reaction we get the value of 'K₃'.

If the equation is reversed then equilibrium constant will be reverse.

If the equation is multiplied by a factor of '(1/2)', the equilibrium constant will be the power of the equilibrium constant of initial reaction.

If the two equations are added then equilibrium constant will be multiplied.

Thus, the value of 'K₃' will be:

`K_3=(1)/((K_2)^(1/2))* K_1`

`K_3=\frac{K_1}{\sqrt {K_2}}`

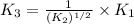
Now put all the given values in this expression, we get:

`K_3=(10^2)/(\sqrt (10^(-4)))`

`K_3=10^4`

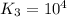
Therefore, the value of K for the reaction 3 will be,
`10^4`