So we have 1280,640,320,...
This is a geometric sequence with the first term,
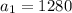
. To find the common ratio r, we are going to divide any current term by a previous one:
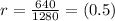
Remember that the main formula of a geometric sequence is:
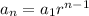
Where

is the nth term (in our case 40),

is the first term (in our case 1280),

is the common ratio (0.5), and

is the position of the term in the sequence (in our case our weeks)
Now we can replace the values to get:

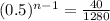
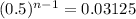
Since our variable, n, is the exponent, we are going to use logarithms to bring it down:
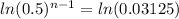
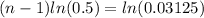
The only thing left now is solving for n to find our week:
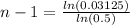
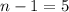

We can conclude that in the sixth week the cafeteria will sell 40 slices of pizza.