Question

Point A is located at (5, 10) and point B is located at (20, 25).

What point partitions the directed line segment AB into a 3:7 ratio?




(9 1/2, 14 1/2)

(9 1/2, 20 1/2)

​(15 1/2, 14 1/2)​

​(15 1/2, 20 1/2)​

Answer 1

Answer: The answer is 9 1/2 and 14 1/2

Answer 2

`(9(1)/(2), 14(1)/(2))`

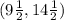
Explanation:

The given points are
`A(5,10)` and
`B(20,25)`.

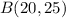We want to find the coordinates of the point that partitions the directed line segment AB into a 3:7 ratio.

The point that partitions a directed line segment into a
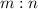`m:n` ratio is given by the formula;

`((mx_2+nx_1)/(m+n), (my_2+ny_1)/(m+n))`

We substitute the given points and evaluate to obtain;

`((3(20)+7(5))/(3+7), (3(25)+7(10))/(3+7))`

`\Rightarrow ((60+35)/(10), (75+70)/(10))`

`\Rightarrow ((95)/(10), (145)/(10))`

`\Rightarrow (9(1)/(2), 14(1)/(2))`

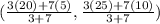
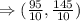
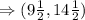
The correct answer is A.