Question

A nationwide test taken by high school sophomores and juniors has three sections, each scored on a scale of 20 to 80. In a recent year, the national mean score for the writing section was 50.4. Based on this information, complete the following statements about the distribution of the scores on the writing section for the recent year.

A) According to Chebyshev theorem, at least (56%,75%,84% 89% Pick which one) or the scores lie within 2 standard deviations of the mean 50.4.
B) Suppose that the distribution is bell-shaped. If approximatly 68% of the scores lie between 40.5 and 60.3, then the approximate value of the standard deviation for the distribution, according to the empirical rule is

Answer 1

According to Chebyshev's theorem, at least 75% of the scores lie within 2 standard deviations of the mean 50.4. According to the empirical rule, if approximately 68% of the scores lie between 40.5 and 60.3, then the standard deviation for the distribution is approximately 4.95.

Step-by-step explanation:

A) According to Chebyshev's theorem, at least 75% of the scores lie within 2 standard deviations of the mean 50.4.

B) According to the empirical rule, if approximately 68% of the scores lie between 40.5 and 60.3, then the standard deviation for the distribution is approximately (60.3 - 50.4) / 2 = 4.95.

Answer 2

a) At least 75% of the scores lie within 2 standard deviations of the mean.

b) The approximate value of the standard deviation would be 9.9.

Step-by-step explanation:

Normal distribution:

Empirical rule, which states that:

68% of the measures are within 1 standard deviation of the mean.

95% of the measures are within 2 standard deviation of the mean.

99.7% of the measures are within 3 standard deviations of the mean.

Non-normal distribution:

Chebyshev Theorem, which states that:

At least 75% of the measures are within 2 standard deviations of the mean.

At least 89% of the measures are within 3 standard deviations of the mean.

An in general terms, the percentage of measures within k standard deviations of the mean is given by
`100(1 - (1)/(k^(2)))`.

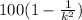A) According to Chebyshev theorem, at least (56%,75%,84% 89% Pick which one) or the scores lie within 2 standard deviations of the mean 50.4.

At least 75% of the scores lie within 2 standard deviations of the mean.

B) Suppose that the distribution is bell-shaped. If approximatly 68% of the scores lie between 40.5 and 60.3, then the approximate value of the standard deviation for the distribution, according to the empirical rule is

68% of the scores lie within 1 standard deviation of the mean.

This means that the standard deviation can be given by:

(60.3 - 40.5)/2 = 9.9

The approximate value of the standard deviation would be 9.9.