Answer:
10 blocks
Explanation:
Noam walks home from school by walking towards North= 8 blocks
Noam walks home from school by walking towards East= 6 blocks
we have to find the shortest path or a direct path from school to his house
We can find it by using Pythagoras theorem,
Hence, shortest or direct path from school to his house=
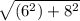
Hence, shortest or direct path from school to his house=
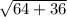
Hence, shortest or direct path from school to his house=
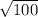 blocks
blocks
Hence, shortest or direct path from school to his house=10 blocks