Question

Calculus help with the graph of a integral and finding the following components.

Answer 1

a)


`\bf \displaystyle F(x)=\int\limits_(4)^(√(x))\cfrac{2t-1}{t+2}\cdot dt\qquad x=16\implies \displaystyle F(x)=\int\limits_(4)^(√(16))\cfrac{2t-1}{t+2}\cdot dt \\\\\\ \displaystyle F(x)=\int\limits_(4)^(4)\cfrac{2t-1}{t+2}\cdot dt\implies 0`

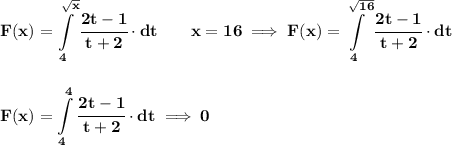
why is 0? well, the bounds are the same.


b)

let's use the second fundamental theorem of calculus, where F'(x) = dF/du * du/dx


`\bf \displaystyle F(x)=\int\limits_(4)^(√(x))\cfrac{2t-1}{t+2}\cdot dt\implies F(x)=\int\limits_(4)^{x^{(1)/(2)}}\cfrac{2t-1}{t+2}\cdot dt\\\\ -------------------------------\\\\ u=x^{(1)/(2)}\implies \cfrac{du}{dx}=\cfrac{1}{2}\cdot x^{-(1)/(2)}\implies \cfrac{du}{dx}=\cfrac{1}{2√(x)}\\\\ -------------------------------\\\\`


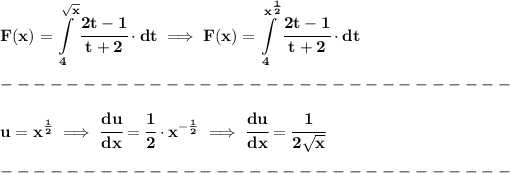
`\bf \displaystyle F(x)=\int\limits_(4)^(u)\cfrac{2t-1}{t+2}\cdot dt\qquad F'(x)=\cfrac{dF}{du}\cdot \cfrac{du}{dx} \\\\\\ \displaystyle\cfrac{d}{du}\left[ \int\limits_(4)^(u)\cfrac{2t-1}{t+2}\cdot dt \right]\cdot \cfrac{du}{dx}\implies \cfrac{2u-1}{u+2}\cdot \cfrac{1}{2√(x)} \\\\\\ \cfrac{2√(x)}{√(x)+2}\cdot \cfrac{1}{2√(x)}\implies \cfrac{2√(x)-1}{2x+4√(x)}`


c)

we know x = 16, we also know from section a) that at that point f(x) = y = 0, so the point is at (16, 0), using section b) let's get the slope,


`\bf \left. \cfrac{2√(x)-1}{2x+4√(x)} \right|_(x=16)\implies \cfrac{2√(16)-1}{2(16)+4√(16)} \implies \cfrac{7}{48}\\\\ -------------------------------\\\\ \begin{cases} x=16\\ y=0\\ m=(7)/(48) \end{cases}\implies \stackrel{\textit{point-slope form}}{y- y_1= m(x- x_1)}\implies y-0=\cfrac{7}{48}(x-16) \\\\\\ y=\cfrac{7}{48}x-\cfrac{7}{3}\implies y=\cfrac{7}{48}x-2(1)/(3)`


d)


`\bf 0=\cfrac{2√(x)-1}{2x+4√(x)}\implies 0=\cfrac{2√(x)-1}{(√(x)+2)(2√(x))}`

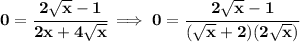
now, we can get critical points from zeroing out the derivative, we also get critical points from zeroing out the denominator, however, the ones from the denominator are points where the function is not differentiable, namely, is not a smooth curve, is a sharp jump, a cusp, or a spike, and therefore those points are usually asymptotic, however, they're valid critical points, let's check both,


`\bf 0=\cfrac{2√(x)-1}{2x+4√(x)}\implies 0=\cfrac{2√(x)-1}{(√(x)+2)(2√(x))}\\\\ -------------------------------\\\\ 0=2√(x)-1\implies 1=2√(x)\implies \cfrac{1}{2}=√(x)\implies \left(\cfrac{1}{2} \right)^2=x \\\\\\ \boxed{\cfrac{1}{4}=x}\\\\ -------------------------------\\\\ 0=(√(x)+2)(2√(x))\implies 0=2√(x)\implies \boxed{0=x} \\\\\\ 0=√(x)+2\implies -2=√(x)\implies (-2)^2=x\implies \boxed{4=x}`

now, doing a first-derivative test on those regions, we get the values as in the picture below.

so, you can see where is increasing and decreasing.