Question

A ball is dropped from rest from the top of a building of height h. At the same instant, a second ball is projected vertically upward from ground level, such that it has zero speed when it reaches the top of the building.

(a) When do the two balls pass each other?
(b) Which ball has greater speed when they are passing?
(c) What is the height of the two balls when they are passing?

Answer 1

a)
`t = \sqrt{(h)/(2g)}`

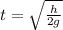
b) Ball 1 has a greater speed than ball 2 when they are passing.

c) The height is the same for both balls = 3h/4.

Step-by-step explanation:

a) We can find the time when the two balls meet by equating the distances as follows:

`y = y_{0_(1)} + v_{0_(1)}t - (1)/(2)gt^(2)`

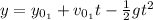
Where:

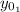`y_{0_(1)}`: is the initial height = h

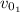`v_{0_(1)}`: is the initial speed of ball 1 = 0 (it is dropped from rest)

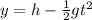`y = h - (1)/(2)gt^(2)` (1)

Now, for ball 2 we have:

`y = y_{0_(2)} + v_{0_(2)}t - (1)/(2)gt^(2)`

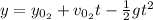
Where:

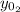`y_{0_(2)}`: is the initial height of ball 2 = 0

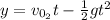`y = v_{0_(2)}t - (1)/(2)gt^(2)` (2)

By equating equation (1) and (2) we have:

`h - (1)/(2)gt^(2) = v_{0_(2)}t - (1)/(2)gt^(2)`

`t=\frac{h}{v_{0_(2)}}`

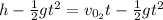
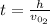
Where the initial velocity of the ball 2 is:

`v_{f_(2)}^(2) = v_{0_(2)}^(2) - 2gh`

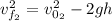
Since
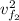`v_{f_(2)}^(2)` = 0 at the maximum height (h):

`v_{0_(2)} = √(2gh)`

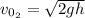
Hence, the time when they pass each other is:

`t = (h)/(√(2gh)) = \sqrt{(h)/(2g)}`

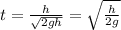
b) When they are passing the speed of each one is:

For ball 1:

`v_{f_(1)} = - gt = -g*\sqrt{(h)/(2g)} = - 0.71√(gh)`

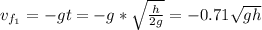
The minus sign is because ball 1 is going down.

For ball 2:

`v_{f_(2)} = v_{0_(2)} - gt = √(2gh) - g*\sqrt{(h)/(2g)} = (√(1) - (1)/(√(2)))*√(gh) = 0.41√(gh)`

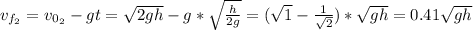
Therefore, taking the magnitude of ball 1 we can see that it has a greater speed than ball 2 when they are passing.

c) The height of the ball is:

For ball 1:

`y_(1) = h - (1)/(2)gt^(2) = h - (1)/(2)g(\sqrt{(h)/(2g)})^(2) = (3)/(4)h`

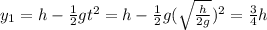
For ball 2:

`y_(2) = v_{0_(2)}t - (1)/(2)gt^(2) = √(2gh)*\sqrt{(h)/(2g)} - (1)/(2)g(\sqrt{(h)/(2g)})^(2) = (3)/(4)h`

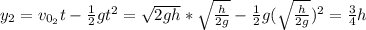
Then, when they are passing the height is the same for both = 3h/4.

I hope it helps you!