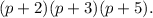Question

Find the lowest common denominator of p+3/p^2+7p+10 and p+5/p^2+5p+6

Answer 1

the answer would be known as (P+5) (P+2) (P+3)

Answer 2

Answer: The lowest common denominator of the given fractions is
`(p+2)(p+3)(p+5).`

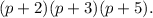
Step-by-step explanation: We are given to find the lowest common denominator of the following fractions :

`F_1=(p+3)/(p^2+7p+10),\\\\\\F_2=(p+5)/(p^2+5p+6).`

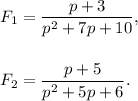
To find the lowest common denominator, we need to factorize the denominators of both the fractions and take the L.C.M. of them.

We have

`F_1=(p+3)/(p^2+7p+10)=(p+3)/(p^2+5p+2p+10)=(p+3)/((p+2)(p+5)),\\\\\\F_2=(p+5)/(p^2+5p+6)=(p+5)/(p^2+3p+2p+6)=(p+5)/((p+2)(p+3)).`

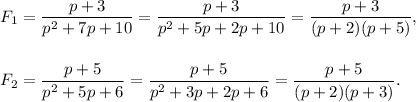
Now, the L.C.M. of the denominators is given by

`L.C.M.\{(p+2)(p+5),(p+2)(p+3)\}=(p+2)(p+3)(p+5).`

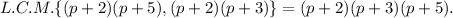
Thus, the lowest common denominator of the given fractions is
`(p+2)(p+3)(p+5).`