Answer:
A.
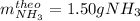
B.
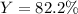
Step-by-step explanation:
Hello!
In this case, since the undergoing chemical reaction between nitrogen and hydrogen is:
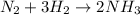
Thus we proceed as follows:
A. Here, we first need to compute the moles of ammonia yielded by each reactant, in order to identify the limiting one:
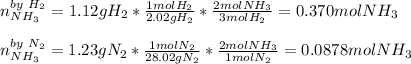
Thus, since nitrogen yields the fewest moles of ammonia, we realize it is the limiting reactant, so the theoretical yield, in grams, of ammonia is:
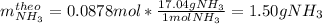
B. Finally, since the actual yield of ammonia is 1.23, the percent yield turns out:
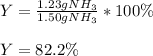
Best regards!