Answer:
f(x) and g(x) have the same domain but different ranges.
Explanation:
The domain of
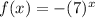 is:
is:
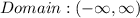
Because there is no any restriction. And its range is:

Because the minus sign is out of the parentheses, so no matter the value of x, the result will be always negative.
Now, The domain of
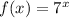 is:
is:
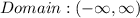
As before, because there is no any restriction. And its range is:
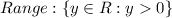
Because no matter the value of x this function is always positive since:
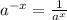
Therefore:
f(x) and g(x) have the same domain but different ranges.
I attached you the graphs.