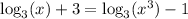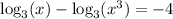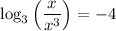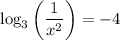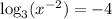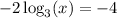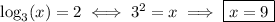Answer:
See below
Explanation:
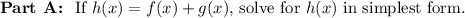
We have
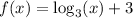
and
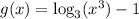
Thus
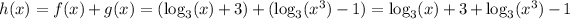
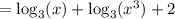
Recall the property of logarithms:
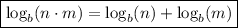
then,
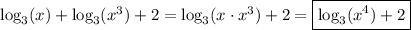
================================================================
I am assuming that the system of equations is
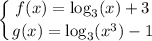
and you probably want the solution when
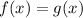 I will name it
I will name it
 , thus
, thus
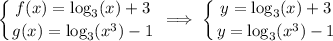
We should just solve