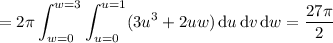Question

Find the outward flux of the vector field f=(x3,y3,z2) across the surface of the region that is enclosed by the circular cylinder x2+y2=1 and the planes z=0 and z=3.

Answer 1

Since the region is closed, we can apply the divergence theorem.


`\mathbf f(x,y,z)=(x^3,y^3,z^2)\implies \\abla\cdot\mathbf f=(\partial(x^3))/(\partial x)+(\partial(y^3))/(\partial y)+(\partial(z^2))/(\partial z)=3x^2+3y^2+2z`

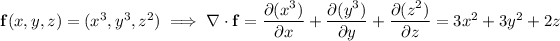
The divergence theorem states that the flux of
`\mathbf f` across a surface
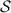
`\mathcal S` enclosing a region
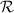
`\mathcal R` is equivalent to the volume integral of
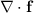
`\\abla\cdot\mathbf f` (the divergence of
`\mathbf f` over
`\mathcal R`:


`\displaystyle\iint_(\mathcal S)\mathbf f\cdot\mathrm d\mathbf S=\iiint_(\mathcal R)(3x^2+3y^2+2z)\,\mathrm dV`

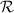
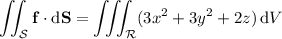
To compute the integral, we convert to cylindrical coordinates using


`x=u\cos v`

`y=u\sin v`

`z=w`

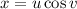
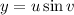
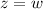
so that
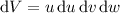
`\mathrm dV=u\,\mathrm du\,\mathrm dv\,\mathrm dw`. Now the integral becomes


`\displaystyle\iiint_(\mathcal R)\\abla\cdot\mathbf f\,\mathrm dV=\int_(w=0)^(w=3)\int_(v=0)^(v=2\pi)\int_(u=0)^(u=1)(3u^2\cos^2v+3u^2\sin^2v+2w)u\,\mathrm du\,\mathrm dv\,\mathrm dw`

`=2\pi\displaystyle\int_(w=0)^(w=3)\int_(u=0)^(u=1)(3u^3+2uw)\,\mathrm du\,\mathrm dv\,\mathrm dw=\frac{27\pi}2`