Question

Determine the values of the constants r and s such that i(x, y) = x rys is an integrating factor for the given differential equation. y(7xy2 + 6) dx + x(xy2 − 1) dy = 0

Answer 1

`\underbrace{y(7xy^2+6)}_(M(x,y))\,\mathrm dx+\underbrace{x(xy^2-1)}_(N(x,y))\,\mathrm dy=0`

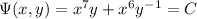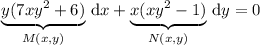
For the ODE to be exact, we require that
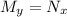
`M_y=N_x`, which we'll verify is not the case here.


`M_y=21xy^2+6`

`N_x=2xy^2-1`

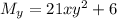
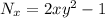
So we distribute an integrating factor
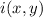
`i(x,y)` across both sides of the ODE to get


`iM\,\mathrm dx+iN\,\mathrm dy=0`

Now for the ODE to be exact, we require
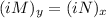
`(iM)_y=(iN)_x`, which in turn means


`i_yM+iM_y=i_xN+iN_x\implies i(M_y-N_x)=i_xN-i_yM`

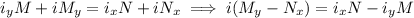
Suppose
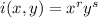
`i(x,y)=x^ry^s`. Then substituting everything into the PDE above, we have


`x^ry^s(19xy^2+7)=rx^(r-1)y^s(x^2y^2-x)-sx^ry^(s-1)(7xy^3+6y)`

`19x^(r+1)y^(s+2)+7x^ry^s=rx^(r+1)y^(s+2)-rx^ry^s-7sx^(r+1)y^(s+2)-6sx^ry^s`

`19x^(r+1)y^(s+2)+7x^ry^s=(r-7s)x^(r+1)y^(s+2)-(r+6s)x^ry^s`

`\implies\begin{cases}r-7s=19\\r+6s=-7\end{cases}\implies r=5,s=-2`

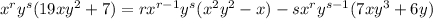
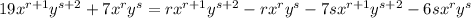
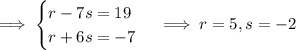
so that our integrating factor is
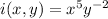
`i(x,y)=x^5y^(-2)`. Our ODE is now


`(7x^6y+6x^5y^(-1))\,\mathrm dx+(x^7-x^6y^(-2))\,\mathrm dy=0`

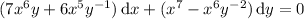
Renaming
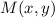
`M(x,y)` and
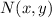
`N(x,y)` to our current coefficients, we end up with partial derivatives


`M_y=7x^6-6x^5y^(-2)`

`N_x=7x^6-6x^5y^(-2)`

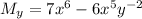
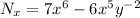
as desired, so our new ODE is indeed exact.

Next, we're looking for a solution of the form
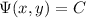
`\Psi(x,y)=C`. By the chain rule, we have


`\Psi_x=7x^6y+6x^5y^(-1)\implies\Psi=x^7y+x^6y^(-1)+f(y)`

Differentiating with respect to
`y` yields


`\Psi_y=x^7-x^6y^(-2)=x^7-x^6y^(-2)+(\mathrm df)/(\mathrm dy)`

`\implies(\mathrm df)/(\mathrm dy)=0\implies f(y)=C`

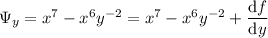
Thus the solution to the ODE is


`\Psi(x,y)=x^7y+x^6y^(-1)=C`