Question

When multiplied out, the number 2018! = 1 ∙ 2 ∙ 3 ∙∙∙ 2016 ∙ 2017 ∙ 2018 ends in a string of zeros. how many zeros are at the end of this number?

Answer 1

The question can be asked in the following form, which is an equivalent
form:
How many multiples of 10 that are less than 2018.
Multiple of 10 are in the form
`10* n`
If the above number is less than 2018, then we get the equation:

`10* n<2018`
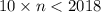
We will solve the above inequality like this:

`n<201.8`
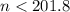
We deduce the following:

There are 201 zeros at the end of 2018!.

Answer 2

The number of zeros at the end of factorial is equal to the number of times powers of 5 can be divided into the number having its factorial calculated, since every one of these 5s can be paired with a 2 to make a 10, giving an additional end zero. The floors for division of powers of five are: 2018 / 5 = 403, 2018 / 25 = 80, 2018 / 125 = 16, 2018 / 625 = 3. 403+80+16+3=502. Thus 2018! has 502 zeros at the end.