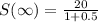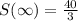Question

Calculate the sum of the infinite series S(infinity)=20-10+5-...

Answer 1

Answer: A. S(\infty)=40/3

Explanation:

Answer 2

`S(\infty)=(40)/(3)`

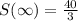
Explanation:

we are given series as

S(infinity)=20-10+5-..

Firstly, we will check type of series

first term=20

second term=-10

third term =5

now, we can find common ratios

`r=(-10)/(20) =-0.5`

`r=(5)/(-10) =-0.5`

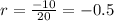
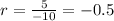
we can see that both ratios are equal

so, this is geometric series

we can use sum of infinite terms formula

`S(\infty)=(a)/(1-r)`

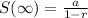
where a is first term

a=20

r=-0.5

now, we can plug values

`S(\infty)=(20)/(1+0.5)`

`S(\infty)=(40)/(3)`