Question

How are rational exponents and radicals related? What procedures are followed to rewrite expressions involving radicals and rational exponents?

What are the key features of the graphs exponential functions? Explain how you find each key feature and what happens to the graphs if you were to add or subtract a constant term.

How can you distinguish between linear and exponential functions? How do increasing linear functions and exponential growth functions compare?

Explain the differences between adding and multiplying radical expressions.

Consider the following non-perfect square number (instructor provides a large number, ex: 1260). Explain whether you would choose the greatest perfect square method or the prime factor method, and then find the simplified square root of that number. (listen to student response) How did you decide to choose that method? Would the other method work? Why or why not?

George plays basketball in a week-long camp. On day 2, he scored 8 points. On day 4, he scored 12 points. Explain how to measure his average rate of change. (Instructors can change the scenario to personalize for the students.)

Give an example of a Geometric and an Arithmetic Sequence. What are the differences between each?

How are the parameters of functions derived from their context?

Answer 1

1. Well, for one they both have a 'radicand' and you can arrange both of them in a fraction form.

2. Graph is increasing, there's an asymptotic value, the domain is all real numbers, the range is y > 0. If you add a constant, you are shifting it vertically, which means it's y-intercept will change by the magnitude of the constant.

3. Linear functions are a straight line with one definite slope. Exponential functions are basically curves with their slopes, not constantly, but changing. As you increase your x-values, the linear functions lacks behind, and the exponential one becomes very large.

4. I really don't know how to explain this, it's kind of confusing.

5. You can use the slope formula: (y2-y1)/(x2-x1). Plug in values, you get:
(12-8)/(4-2). This can be simplified to 4/2 or just 2. That's his average rate of change: 2 balls per day.

6. An arithmetic sequence adds on a specific value every time. For example: {1, 3, 5, 7...}
A Geometric sequence increases every time by a common ratio. For example: {2, 6, 18, 54...}

6. If it's relative to time, then you have a parametric equation dealing with time. Just like that, you can see that 1 variable changes with respect to the other, and that implies parametricity.

Answer 2

1) Every radical can be rewritten has an exponent 2) Domain, Range, Base, and Asymptote.

Step by Step Explanation:

1) As a matter of fact every radical, is a number or an expression with a rational exponent. Therefore, it is a equality relationship, like this:

If √a=
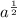`a^{(1)/(2)}` then
`\sqrt[3]{a^(2) }`=1^(2/3)

That is the procedure: the radicand is the base; the numerator is the exponent to that radicand is raised to. In addition, the denominator is the index of the root.

2) Since the Exponential Function has this form:

`f(x)=c^(ax+b)+k`

We can algebraically see that there is no restriction to the Domain, since the x can assume any value. And the function is a continuous one.

`y=c^(x)\\  c^x=?\\ D={...,c^(-1) =((1)/(c)),\\c^0=1,\\ c^1=c, ...}`

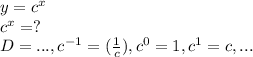
As for the Range

Since the base must always be greater than 0 and 1, considering an exponential form in this way:

`f(x)=c^(ax+b)+k` like y=
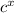`c^(x)` since k=0 y must always be greater than zero, therefore y >0

Base

We cannot have a power which its base is 0, since any value for x would result in the same result for y.

`y=0^0, 0^1=0, 0^2=0,0^3=0`

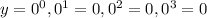
Similarly we cannot have a base as 1, since 1^0=1,1^1=1 What would give us not an exponential function.

Asymptote

The asymptote is given by the constant k,
`f(x)=c^(ax+b)+k`, whether it is zero or any other value.

y=k for (Horizontal) Asymptote

Whenever we add a positive constant or subtract a constant It happens like in that picture below.

3) By the increasing or decreasing rate since, among the polynomial ones the exponential has the quickest growth. Check it out.

4) This is visually explained

5) In order to obtain a simplified radical of that square root, the Prime Factors must be choosen. The Greatest Perfect is aimed for those cases in which we want the value in decimal form.

6) Let us call our Domain (d) Days and Range as (Points).

So

Days(d) Points (P)

2 4

4 12

We can measure this rate of change, by calculating the angular coefficient

`m=\frac{P_(2)-P_(1)}{D_(2)-D{1}}`

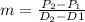
Plugging in the Values

`m=(12-4)/(4-2) =4`

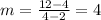
7) An Arithmetic Sequence is a Sequence that increases, decreases, or even maintain itself at linear rate and a Geometric Sequence increases, decreases, or even may maintain itself exponentially

A ={10,12,14,16,…}

G={10,100,1000,10000,…}

8) Through observation, of patterns and changing whether it is a fast changing or even constant. We can derive parameters of functions from their context, time, and others