We have to complete the statement:
" The rate of change in the function y=x+4 is ______ the rate of change of the function represented in the table."
Let us consider the function represented in table.
The coordinates given in the table are:
(0,6) (2,8) (4,10) and (6,12)
Consider the first two coordinates (0,6) and (2,8)
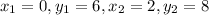
Equation of line is given by
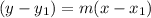
where 'm' is slope(rate of change) is given by the formula:
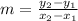
So,
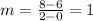
So, equation of line is :
(y-6)= 1 (x-0)
y-6=x
y=x+6
Comparing it with standard equation of line y=mx+c with slope 'm'.
So, we get m(Rate of change)=1.
Now,
We will find the rate of change(slope) in the function y=x+4
Comparing it with standard equation of line y=mx+c with slope 'm'.
So, we get m(Rate of change)=1.
So, " The rate of change in the function y=x+4 is equal to the rate of change of the function represented in the table.