Question

Write an equation of the line that passes through the given points. (-2,8) and (1,2)

(Write answer in slope-intercept form.)

Answer 1

the answer is y= -1/2x-7

Answer 2

The slope-intercept form of the line that passes through the points (-2,8) and (1,2) is y=-2x+4

Explanation:

Given:

Points(x,y)= )= (-2,8)

Points(x1,y1)= (1,2)

To find:

Equation in slope-intercept form=?

Solution:

The slope intercept form of a line is y= mx + b

Where m= the slope

STEP 1: Finding the slope value

`\bold{\text { slope } =(y-y 1)/(x-x 1)}`

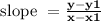
Substituting the points in the formula we get,

`\text {slope, } \quad m=(2-8)/(1-(-2))`

`\text {slope, } \quad m=(-6)/(3)`

`\text { slope, } \quad m=-2`

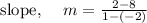
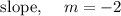
STEP 2: Finding the value of b

Substituting the slope value in the equation we have

y=mx+b,

y= -2(x)+b

y= -2(x) + b

substituting x and y from the points given,

8=-2(-2) + b

8=4+b

8-4=b

b =4

STEP 3: Formation of slope intercept equation

Substituting b and m in the equation of slope we get,

y= mx + b

y= -2x+4.