QUESTION 1
The given system of equation is
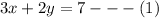
and
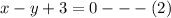
The question requires that, we make x the subject in equation (2) and put it inside equation (1).
So let us express x in terms of y in equation (2) and call it equation (3) to get,
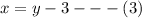
We now substitute equation (3) in to (1) to obtain,
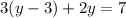
Therefore the correct answer is B.
QUESTION 2
The given equations are
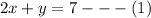
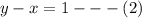
First let us make all the four possible substitutions.
The first is to make y the subject in equation (2) and substitute in to equation (1) to get,
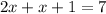
The second one is to make x the subject in equation (2) and put in to equation (1) to get,
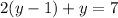
The third one is to make y the subject in equation (1) and put it into equation (2) to get,

The fourth one is to make x the subject in equation (1) and put it in to equation (2) to get,
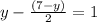
By comparing to given options, C is not part of the four possible results.
Therefore the correct answer is option C.
QUESTION 3
The equations are
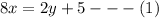
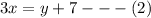
We make y the subject in equation (2) to get,
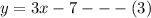
We substitute equation (3) in to equation (1) to get,
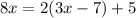
We expand to obtain,
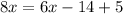
We group like terms to get,
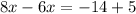
This implies that,
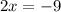
Therefore,

We substitute this value into equation (3) to get,
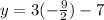
This implies that,

This gives us,
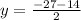
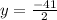
The solution set is
{
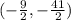
}
The correct answer is B.