Answer:
B.
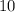 cm,
cm,
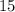 cm,
cm,
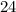 cm
cm
Explanation:
we know that
The Triangle Inequality Theorem, states that the sum of the lengths of two sides of a triangle must always be greater than the length of the third side
so
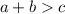
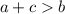
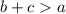
where
a,b,c are the lengths sides of the triangle
case A)
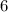 cm,
cm,
 cm,
cm,
 cm
cm
Let
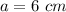
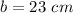
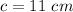
Verify
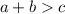 ------>
------>
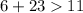 ------> is true
------> is true
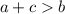 ------>
------>
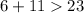 -------> is not true
-------> is not true
therefore
The three lengths of case A) could not be the lengths of the sides of a triangle
case B)
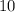 cm,
cm,
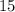 cm,
cm,
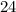 cm
cm
Let
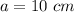
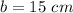
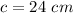
Verify
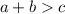 ------>
------>
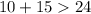 ------> is true
------> is true
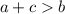 ------>
------>
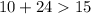 -------> is true
-------> is true
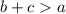 ----->
----->
 --------> is true
--------> is true
therefore
The three lengths of case B) could be the lengths of the sides of a triangle
case C)
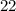 cm,
cm,
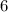 cm,
cm,
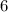 cm
cm
Let

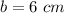
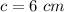
Verify
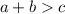 ------>
------>
 ------> is true
------> is true
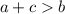 ------>
------>
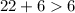 -------> is true
-------> is true
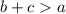 ----->
----->
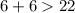 --------> is not true
--------> is not true
therefore
The three lengths of case C) could not be the lengths of the sides of a triangle
case D)
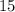 cm,
cm,
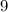 cm,
cm,
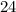 cm
cm
Let
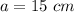

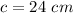
Verify
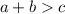 ------>
------>
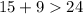 ------> is not true
------> is not true
therefore
The three lengths of case D) could not be the lengths of the sides of a triangle