Answer:
Option C
Statement
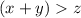 is true
is true
Explanation:
Given the lengths of sides of triangle are x, y, and z.
and also given that
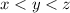
As per the triangle inequality states that the sum of two sides of the triangle is always greater than the measure of third side.
The only condition for this triangle inequality from the given option be
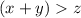
For example:
let x= 3 unit , y= 4 unit and z= 5 unit and
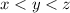 i,e
i,e
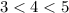 .
.
then,
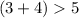
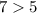 true.
true.
therefore, the only statement C is true.